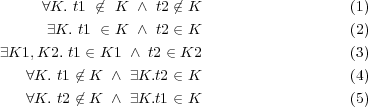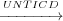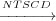Also available as: PDF.
Control Dependence for Extended Finite State Machines
WC2R 2LS, United Kingdom.
{kalliopi.androutsopoulos, david.j.clark, mark.harman, zheng.li}@kcl.ac.uk
2Bournemouth University, Poole, Dorset, BH12 5BB, United Kingdom. laurie@tratt.net
1 Introduction
Program slicing is a source code analysis technique that identifies the parts of a program’s source code which can affect the computation of a chosen variable at a chosen point in it. The variable and point of interest constitute the slicing criterion. There are many variations on the slicing theme. For instance, slices can be constructed statically (with respect to all possible inputs), dynamically (with respect to a single input) or within some spectrum in-between. Program slicing has proved to be widely applicable, with application areas ranging from program comprehension [HBD03] to reverse engineering and reuse [CCD98].
However, despite thirty years of research, several hundred papers and many surveys on program slicing [BH04, De 01, Tip95], there has been comparatively little work on slicing at the model level. This paper tackles slicing at the model level, particularly static slicing of Finite State Machines (FSMs).
FSMs are a graphical formalism that have become widely used in specifications of embedded and reactive systems. Their main drawback is that even moderately complicated systems result in large and unwieldy diagrams. Harel’s Statecharts [Har87] and Extended Finite State Machines (EFSMs) are two of the many attempts over past decades to address FSM’s disadvantages.
Work on slicing FSM models began with the work of Heimdahl et al. in the late 1990s [HW97, HTW98], followed by Wang et al. [WDQ02] and then in 2003 by the work of Korel et al. [KSTV03] and more recently by Langenhove and Hoogewijs [LH07] and by Labbé et al. [LGP07, LG08].
One of the challenges facing any attempt to slice an EFSM is the problem of how to correctly account for control dependence. It is common for state machines modelling such things as reactive systems not to have a final computation point or ‘exit node’. To overcome this problem, Ranganath et al. [RAB+05] recently introduced the concept of a control sink and associated control dependence definitions for reactive programs. A control sink is a strongly connected component from which control flow cannot escape once it enters. Building on this, Labbé et al. [LGP07, LG08] introduced a notion of control dependence and an associated slicing algorithm for EFSMs that was non-termination sensitive. However, they introduce a syntax dependent condition and thus cannot be applied to any FSM.
However, traditional control dependence, as used in program slicing [HRB90] is non-termination insensitive, with the consequence that the semantics of a program slice dominates the semantics of the program from which it is; slicing may remove non-termination, but it will never introduce it. In moving slicing from the program level to the state based model level, an important choice needs to be made
“should EFSM slicing be non-termination sensitive or insensitive?”
Recent work on control dependence has only considered the non-termination sensitive option [LGP07, LG08]. The non-termination insensitive option was explored by Korel et al. [KSTV03], but only for the restricted class of state machines that guarantee to have an exit state. Heimdahl et al. [HW97, HTW98] have a different notion of control dependence which is not a structural property of the graph of FSMs but is based on the dependency relation between events and generated events. This could lead to slices being either non-termination sensitive or insensitive depending on the specification. The definition of control dependence given in [WDQ02, LH07] is for UML statecharts with nested and concurrent states and is the same as that of data dependence when applied to EFSMs that do not have concurrent and/or nested states. This leaves open the question of how to extend control dependence to create non-termination insensitive slicing for general EFSMs in which there may be no exit node.
This problem is not merely of intellectual curiosity as it also has implications for the applications of slicing. In the literature on traditional program slicing, a non-termination sensitive formulation was proposed as early as 1993 by Kamkar [Kam93], but has not been taken up in subsequent slicing research. Non-termination sensitive slicing tends to produce very large slices, because all iterative constructs that cannot be statically determined to terminate must be retained in the slice, no matter whether they have any effect other than termination on the values computed at the slicing criterion. These ‘loop shells’ must be retained in order to respect the definition of non-termination sensitivity. Furthermore, for most of the applications of slicing listed above, it turns out that it is perfectly acceptable for slicing to be non-termination insensitive.
In this paper, we introduce a non-termination insensitive form of control dependence for EFSM dependence analysis, that can be applied to any FSM, and a slicing algorithm based upon it. Like Labbé et al., we build on the recent work of Ranganath et al. [RAB+05], but our definition is non-termination insensitive. Also, unlike Korel’s definition, our development of the recent work of Ranganath et al. allows us to handle arbitrary EFSMs. We prove that our definition of control dependence is backward compatible with traditional non-termination insensitive control dependence outside of control sinks. Furthermore, we prove that our definition agrees with the non-termination sensitive control dependence of Labbé et al. inside control sinks. Finally we demonstrate the type of slices produced with our definition.
2 Extended Finite State Machines
We formally define an EFSM as follows.
Definition 1 (Extended Finite State Machine). An Extended Finite State Machine (EFSM) E=(S, T, Ev, V) where S is a set of states, T is a set of transitions, Ev is a set of events, and V is a store represented by a set of variables. Transitions have a source state source(t) ∈ S, a target state target(t) ∈ S and a label lbl(t). Transition labels are of the form e1[g]∕a where e1 ∈ Ev, g is a guard, i.e. a condition (we assume a standard conditional language) that guards the transition from being taken when an e1 is true, and a is a sequence of actions (we assume a standard expression language including assignments). All parts of a label are optional.
EFSMs are possibly non-deterministic. States of S are atomic. Actions can involve store updates or generation of events or both. A transition t may have a successor t′ whose source is the same as the target of t. Two or more distinct transitions which share the same source node are said to be siblings. A final transition is a transition whose target is an exit state and an exit state is a state which has no outgoing transitions. An ε-transition is one with no event or guard.
3 Survey
In this section we survey several existing definitions of control dependence and discuss their strengths and weaknesses.
Ranganath et al.’s control dependence definitions [RAB+05, RAB+07] are defined for programs of systems with multiple exit points and / or which execute indefinitely, and therefore form the basis for subsequent state machine control dependence definitions. We exclude from this discussion the control dependence definition as given in [WDQ02, LH07] because it is defined in terms of concurrent states and transitions and EFSMs do not have concurrent states and transitions. Moreover, when applied to states and transitions that are not concurrent, it is the same as data dependence as in Definition 13.
Korel et al [KSTV03], Ranganath et al. and Labbé et al. [LGP07, LG08] definitions of control dependence are given in terms of execution paths. Since a path is commonly presented as a (possibly infinite) sequence of nodes, a node is in a path if it is in the sequence. A transition is in a path if its source state is in the path and its target state is both in the path and immediately follows its source state. A maximal path is any path that terminates in an end node or final transition, or is infinite.
3.1 Control flow for RSML
Heimdahl et al. [HW97, HTW98] present an approach for slicing specifications modelled in the Requirements State Machine Language (RSML) [LHHR94], a tabular notation that is based on hierarchical finite state machines. Transitions have events, guards and actions; events can generate events as actions, which are broadcast in the next step of execution. Heimdahl et al. were the first to present a control dependence-like definition for FSMs; it differs from the traditional notion as it defines control flow in terms of events rather than transitions.
Definition 2 (Control flow for RSML (CF) [HTW98]). Let E be the set of all events and T the set of all transitions. The relation trigger(T → E) represents the trigger event of a transition. The relation action(T → E2) represents the set of events that make up the action caused by executing a transition. follows(T → T) is defined as: (t1,t2) ∈ follows iff trigger(t1) ∈ action(t2).
CF can be applied to non-terminating systems that have multiple exit nodes. However, it depends on transitions being triggered by events and being able to generate events as actions and therefore cannot be applied to any finite state machine, such as EFSMs that do not generate events.
3.2 Control dependence for EFSMs
Korel et al. [KSTV03] present a definition of control dependence for EFSMs in terms of post dominance that requires execution paths to lead to an exit state.
Definition 3 (Post Dominance [KSTV03]). Let Y and Z be two states and T be an outgoing transition from Y .
- State Z post-dominates state Y iff Z is in every path from Y to an exit state.
- State Z post-dominates transition T iff Z is on every path from Y to the exit state though T. This can be rephrased as Z post-dominates target(T).
Definition 4 (Insensitive Control Dependence (ICD) [KSTV03]). Transition Tk is control dependent on transition Ti if:
- source(Tk) post-dominates transition Ti (or target(Ti)), and
- source(Tk) does not post-dominate source(Ti).
This definition is successful in capturing the traditional notion of control dependence for static backward slicing. However it can only determine control dependence for state machines with exactly one end state, failing if there are multiple exit states or if the state machine is possibly non-terminating.
3.3 Control dependence for non-terminating programs
Ranganath et al. [RAB+05, RAB+07] address the issue of determining control dependence for programs utilising Control Flow Graphs (CFGs). A CFG is a labelled, directed graph with a set of nodes that represent statements in a program and edges that represent the control flow. A node is either a statement node (which has a single successor) or a predicate node (which has two successors, labelled with T or F for the true and false cases respectively). A CFG has a start node ns (which must have no incoming edges) such that all nodes are reachable from ns; it may have a set of end nodes that have no successors.
Two versions of control dependence definitions are described: non-termination sensitive and non-termination insensitive control dependence. The difference between these definitions lies in the choice of paths. Non-termination sensitive control dependence is given in terms of maximal paths.
Definition 5 (Non-termination Sensitive Control Dependence
(NTSCD)). In a CFG, Ni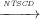 j means that a node Nj is non-termination
sensitive control dependent on a node Ni iff Ni has at least two successors Nk
and Nl such that: for all maximal paths π from Nk, where Nj ∈ π; and there
exists a maximal path π0 from Nl where Nj ⁄∈ π0.
j means that a node Nj is non-termination
sensitive control dependent on a node Ni iff Ni has at least two successors Nk
and Nl such that: for all maximal paths π from Nk, where Nj ∈ π; and there
exists a maximal path π0 from Nl where Nj ⁄∈ π0.
Non-termination insensitive control dependence is given in terms of sink-bounded paths that end in control sinks. A control sink is a region of the graph which, once entered, is never left. These regions are always SCCs, even if only the trivial SCC, i.e. a single node with no successors.
Definition 6 (Control Sink). A control sink, 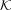 , is a set of nodes that form
a strongly connected component such that, for each node n in
, is a set of nodes that form
a strongly connected component such that, for each node n in 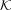 each successor
of n is in
each successor
of n is in 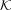 .
.
Definition 7 (Sink-bounded Paths). A maximal path π is sink-bounded iff there
exists a control sink 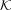 such that:
such that:
- π contains a node from
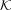 ;
;
- if π is infinite then all nodes in
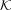 occur infinitely often.
occur infinitely often.
The second clause of Definition 7 defines a form of fairness and hence we refer to it as the fairness condition. SinkPaths(N) denotes a set of sink-bounded paths from a node N. We now define Ranganath et al. [RAB+05] non-termination insensitive version of control dependence.
Definition 8 (Non-termination Insensitive Control Dependence
(NTICD)). In a CFG, Ti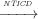 j means that a node Nj is non-termination
insensitive control dependent on a node Ni iff Ni has at least two successors Nk and
Nl such that:
j means that a node Nj is non-termination
insensitive control dependent on a node Ni iff Ni has at least two successors Nk and
Nl such that:
- for all paths π ∈ SinkPaths(Nk) where Nj ∈ π;
- there exists a path π0 ∈ SinkPaths(Nl) where Nj ⁄∈ π0.
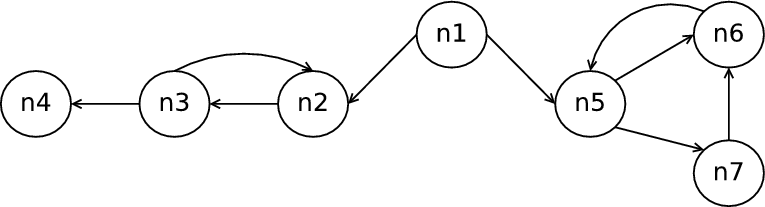
The difference between paths in NTSCD and NTICD is shown in Figure 1. According
to Definition 5, n1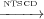 2 and n1
2 and n1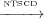 3 but not n1
3 but not n1 4 because n4 is not
in all maximal paths as there is a maximal path with an infinite loop, i.e.
{n2 → n3 → n2...}. However, n1
4 because n4 is not
in all maximal paths as there is a maximal path with an infinite loop, i.e.
{n2 → n3 → n2...}. However, n1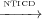 2,n3,n4 since n2,n3 and n4 occur on all
sink-bounded paths from n2 (the control sink for these paths is n4) and there exists a
sink bounded path from n5 (the control sink consists of n5,n6,n7) which does not
include n2,n3 and n4. Compared to NTSCD, NTICD cannot calculate any control
dependencies within control sinks. For example, in Figure 1, n5
2,n3,n4 since n2,n3 and n4 occur on all
sink-bounded paths from n2 (the control sink for these paths is n4) and there exists a
sink bounded path from n5 (the control sink consists of n5,n6,n7) which does not
include n2,n3 and n4. Compared to NTSCD, NTICD cannot calculate any control
dependencies within control sinks. For example, in Figure 1, n5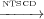 7 but
no such dependency exists for NTICD. Some programs (e.g. servers) are a
global control sink and as such there would be NTSCD, but no NTICD,
dependences.
7 but
no such dependency exists for NTICD. Some programs (e.g. servers) are a
global control sink and as such there would be NTSCD, but no NTICD,
dependences.
3.4 Control dependence for communicating automata
Labbé et al. [LG08]1 adapt Ranganath et al.’s NTSCD definition for communicating automata, in particular focusing on Input/Output Symbolic Transition Systems (IOSTS) [GGRT06].
Definition 9 (Labb? et al.- Non-Termination Sensitive Control Dependence (LG-NTSCD) [LG08]). For an IOSTS S, a transition Tj is control dependent on a transition Ti if Ti has a sibling transition Tk such that:
- Ti has a non-trivial guard, i.e. a guard whose value is not constant under all variable valuations;
- for all maximal paths π from Ti, the source of Tj belongs to π;
- there exists a maximal path π0 from Tk such that the source of Tj does not belong to π0.
FSM models differ from CFGs is several ways. For example, FSMs can have
multiple start and exit nodes, more than two edges between two states and more than
two successors from a state. Moreover, in CFGs, decisions (Boolean conditions)
are made at the predicate nodes while in state machines they are made on
transitions. Labbé et al. take such differences into account when adapting NTSCD.
For example in Figure 2 T2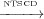 3 and T3
3 and T3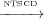 2 because according
to the second clause in Definition 5 the maximal paths start from start.
However these control dependencies are non-sensical because T2 and T3 are
sibling transitions. Using LG-NTSCD these control dependencies do not exist
because in the third clause of Definition 9 the maximal paths start from
s1.
2 because according
to the second clause in Definition 5 the maximal paths start from start.
However these control dependencies are non-sensical because T2 and T3 are
sibling transitions. Using LG-NTSCD these control dependencies do not exist
because in the third clause of Definition 9 the maximal paths start from
s1.
The first clause of LG-NTSCD concerning the non-triviality of guards is introduced in order to avoid a transition being control dependent on transitions that are executed non-deterministically even though they are NTSCD control dependent. Furthermore, because this is a syntax dependent clause, the definition cannot be applied to many FSMs, such as the FSM for the elevator system in Figure 3 that contains transitions with trivial guards.
4 New Control Dependence Definition: UNTICD
We define a new control dependence definition by extending Ranganath et al.’s NTICD definition and subsuming Korel et al.’s definition in order to capture a notion of control dependence for EFSMs that has the following properties. First, the definition is general in that it should be applicable to any reasonable FSM language variant. Second, it is applicable to non-terminating FSMs and / or those that have multiple exit states. Third, by choosing FSM slicing to be non-termination insensitive (in order to coincide with traditional program slicing) it produces smaller slices than traditional non-termination sensitive slicing.
Following [RAB+05], the paths that we consider are sink-bounded paths, i.e. those that terminate in a control sink as in Definition 6. Unlike NTICD, the sink-bounded paths are unfair, i.e. we drop the fairness condition in Definition 7. For non-terminating systems this means that control dependence can be calculated within control sinks.
Definition 10 (Unfair Sink-bounded Paths). A maximal path π is
sink-bounded iff there exists a control sink 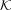 such that π contains a transition
from
such that π contains a transition
from 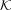 .
.
Note that a transition is in a path if its source state is in the path and its target state is both in the path and immediately follows its source state.
Definition 11 (Unfair Non-termination Insensitive Control Dependence
(UNTICD)). Ti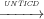 j means that a transition Tj is control dependent on a
transition Ti iff Ti has at least one sibling Tk such that:
j means that a transition Tj is control dependent on a
transition Ti iff Ti has at least one sibling Tk such that:
- for all paths π ∈ UnfairSinkPaths(target(Ti)), the source(Tj) belongs to π;
- there exists a path π ∈ UnfairSinkPaths(source(Tk)) such that the source(Tj) does not belong to π.
UNTICD is in essence a version of NTICD modified to EFSMs (rather than CFGs)
and given in terms of unfair sink-bounded paths. This means that, unlike in the
second clause of Definition 8, sink-bounded paths start from the source of Tk
rather than from the target of Tk because EFSMS can have many transitions
between states and Definition 8 would lead to non-sensical dependences, e.g. in
Figure 2 T2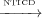 3 while according to our definition T2 does not control
T3.
3 while according to our definition T2 does not control
T3.
5 Properties of the Control Dependence Relation
We prove the following properties for UNTICD: UNTICD subsumes ICD; the transitive closure for the NTICD relation is contained in the transitive closure for the UNTICD relation; and for an EFSM M, UNTICD and NTSCD dependences for all transitions within control sinks are identical.
5.1 UNTICD subsumes ICD
Proof. Definition 4 is given in terms of post dominance which considers every path to a unique exit state. Definition 11 is given in terms of sink-bounded paths that terminate in control sinks. The final transition that leads to the exit state is a trivial strongly-connected component that has no successors, and hence is a control sink. Therefore, the paths in ICD are contained in the paths of NTICD, but NTICD is not restricted to these. Moreover, the clauses of definition 4 are the same as the clauses of definition 11. ⊓ ⊔
5.2 Relation between NTICD and UNTICD’s transitive closures
In Theorem 2 we show that the transitive closure of 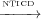 is contained in the
transitive closure of
is contained in the
transitive closure of 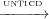 . This shows that UNTICD does not introduce any
additional dependences other than NTICD outside of the control sinks (see Lemma
2) but introduces dependences within control sinks. In order to prove this
theorem, we first need to identify the regions in the state machine where
dependencies can occur and we do that by considering all the cases in which a
transition t1 controls another transition t2, where K, K1, K2 are control
sinks:
. This shows that UNTICD does not introduce any
additional dependences other than NTICD outside of the control sinks (see Lemma
2) but introduces dependences within control sinks. In order to prove this
theorem, we first need to identify the regions in the state machine where
dependencies can occur and we do that by considering all the cases in which a
transition t1 controls another transition t2, where K, K1, K2 are control
sinks:
In case (1) both t1 and t2 are not in any control sink K. In case (2) both t1 and t2 are in the same control sink K. In case (3) t1 is in a control sink K1 and t2 is in another control sink K2. In case (4) t1 is not in any control sink and t2 belongs to a control sink. In case (5) t2 does not belong to any control sink and t1 belongs to a control sink. We introduce Definition 12 that defines a descendant of a transition and the Lemma 1 so that we can discard any impossible cases.
Definition 12 (Descendent). A descendant of t is a transition related to t by the closure of the successor relation.
By Lemma 1, cases (3) and (5) are not possible since t1 can only control t2 if t2 is a descendant of t1. Therefore, we only consider cases (1), (2), and (4). When t1 NTICD controls t2, then for each case we write case1F, case2F, and case4F. Similarly when t1 UNTICD t2, then we write case1U, case2U, and case4U.
Lemma 2 shows that the control dependences produced by applying UNTICD to transitions outside of the control sink are the same as those produced when applying NTICD, i.e. case1U = case1F.
Lemma 2. For an EFSM M, NTICD and UNTICD dependences for transitions T outside of the control sink K (where t ∈ T and t ⁄∈ K), are the same.
Proof. Let us assume that in an EFSM M, Tj is NTICD control dependent
on Ti (Ti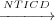 j) and that Ti and Tj are outside of the control sink.
From Definition 8, Ti has a sibling transition Tk such that there exists a path
πk ∈ SinkPaths(Tk) where the source(Tj) does not belong to πk.
j) and that Ti and Tj are outside of the control sink.
From Definition 8, Ti has a sibling transition Tk such that there exists a path
πk ∈ SinkPaths(Tk) where the source(Tj) does not belong to πk.
Now suppose that the fairness condition in the definition of sink bounded paths is removed, i.e. Definition 11 holds, then this affects the transitions within the control sink only in that they do not occur infinitely often. The source of Tj still remains on all paths from Ti as these are outside of the control sink and πk still exists. Therefore, NTICD and UNTICD dependences of transitions outside of the control sink are the same. ⊓ ⊔
The pairwise intersection of case (1), (2), (4) are empty. Therefore the relations can be partitioned as follows:
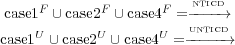
In Theorem 2 we show that the transitive closure of NTICD dependences between transitions within a control sink and between a transition outside of the control sink and a transition within a control sink is a subset of the transitive closure of UNTICD dependences between transitions within a control sink and between a transition outside of the control sink and a transition within a control sink, i.e. (case2F ∪ case4F)* ⊆ (case2U ∪ case4U)*. First we prove the following lemma.
Lemma 3. Let A ∩ B = C ∩ D = ∅ and X = A ∪ B while Y = C ∪ D. If A = C then X*⊆ Y * if B*⊆ D*. All relations are over the same base set.
Proof. (x1,x2) ∈ X* iff there exists a path π ∈ (x1,x2),(x2,x3),...,(xn-1,xn) so that for two successive members (xi,xj) and (xk,xl) ∈ π, xj = xk, and for all (xi,xj) ∈ X. This constructs the smallest transitive closure of X.
We show X*⊆ Y * by induction on the length of the path π in X*.
- Base Case:
- length(π) = 1 then either (x0,x1) ∈ A = C ⊆ (C ∪ D)* = Y * or (x0,x1) ∈ X* because (x0,x1) ∈ B ⊆ B*⊆ D*⊆ (C ∪ D)* = Y *
- Induction Case:
- (Inductive Hypothesis (IH)) Let xX*y because there exists
a path π ∈ xX*x1X*x2...X*y of length N in X*. Then there exists a path
π1 in Y such that xY *y.
Let xX*z because there exists a path π of length N + 1 in X. Then ∃y,z. xX*yXz and by IH xY *y by the same arguments for the base case of yXz then yY *z hence xY *z. ⊓ ⊔
Proof.  *⊆
*⊆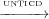 * can also be expressed as the transitive closure for all of
the cases: (case1F ∪ case2F ∪ case4F)*⊆ (case1U ∪ case2U ∪ case4U)* which is true
if:
* can also be expressed as the transitive closure for all of
the cases: (case1F ∪ case2F ∪ case4F)*⊆ (case1U ∪ case2U ∪ case4U)* which is true
if:
- case1F = case1U, i.e. that NTICD and UNTICD dependences between transitions that are not in a control sink are the same, by Lemma 2, and
- (case2F ∪ case4F)* ⊆ (case2U ∪ case4U)*, i.e. that the transitive closure of NTICD dependences between transitions within a control sink and a transition outside of the control sink, and between transitions within a control sink is a subset of the transitive closure of UNTICD dependences between transitions within a control sink and a transition outside of the control sink, and between transitions within a control sink. This is true because of Lemma 3. ⊓ ⊔
5.3 NTSCD and UNTICD dependencies within control sinks
Finally, we show that UNTICD and NTSCD are compatible in control sinks.
Proof. In a control sink K, if Ti ∈ K and Tj ∈ K, then according to Definition 11 sink-bounded paths are reduced to maximal paths, since transitions in K do not occur infinitely often (fairly). This coincides with Definition 5. Therefore, the control dependences produced by UNTICD and NTSCD for transitions within control sinks are equivalent. ⊓ ⊔
6 Comparison of UNTICD with existing definitions
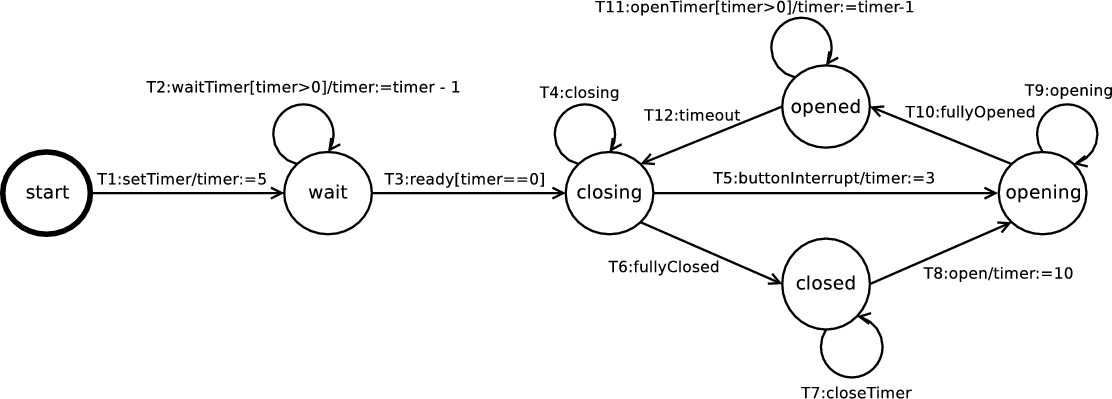
Figure 3 illustrates an EFSM of the door control component, a subcomponent of the elevator control system [SW99]. The door component controls the elevator door, i.e. it opens the door, waits for the passengers to enter or leave the elevator and finally shuts the door. In this section we compute all the control dependencies for this EFSM using the existing and new definitions for the purpose of comparison, as given in Figure 4.
| CF | No dependences as the EFSM does not have generated events
| |
| ICD | Not applicable as the EFSM does not have a unique exit state
| |
| NTSCD | wait → closing | closing → closed |
| closed → opening | opening → opened | |
| opened → closing | closing → opening | |
| NTICD | No dependences
| |
| LG-NTSCD | T3 → T4,T5,T6
| |
| UNTICD | T5 → T9,T10 | T6 → T7,T8 |
| T8 → T9,T10 | T10 → T11,T12 | |
| T12 → T4,T5,T6 | ||
CF cannot be applied to the EFSM in Figure 3 because it is given in terms of the relationship between events and generated events and according to the syntax of EFSMs, events cannot be generated.
ICD cannot be applied to the the EFSM in Figure 3 because it does not have a unique exit state. For EFSMs that lead to a unique exit state the control dependences computed for both ICD and UNTICD are the same. For example, in Figure 2, ICD and UNTICD compute the same dependences, i.e. T1 → T2,T3,T4,T5.
In Figure 4, NTSCD and NTICD are given in terms of nodes but can easily be
represented in terms of transitions. Compared to UNTICD, NTSCD considers
maximal paths rather than sink-bounded paths and consequently introduces more
dependences when there are loops on paths that lead to a control sink. For
example, in Figure 3, wait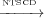 closing because of the loop introduced
by the self-transition T2. Note that NTSCD and UNTICD have the same
dependences inside control sinks—we have formally shown this to be true in
Theorem 3.
closing because of the loop introduced
by the self-transition T2. Note that NTSCD and UNTICD have the same
dependences inside control sinks—we have formally shown this to be true in
Theorem 3.
In Figure 3 there are no NTICD dependences because any control dependency caused by loops on paths to a control sink are ignored and there are no control dependencies within control sinks because of the fairness condition of sink-bounded paths. Unlike NTICD, UNTICD calculates dependences with control sinks. Also, as formally shown by Theorem 2, the transitive closure of NTICD is contained within the transitive closure of UNTICD, although trivially true in this case.
LG-NTSCD is NTSCD adapted for transitions and with a syntax dependent clause, i.e. that the controlling transition’s guard must be non-trivial. This additional clause reduces the number of dependences compared to those of NTSCD. For example, in Figure 3, T5,T6,T8,T10 and T12 do not control any other transition because they have trivial guards. The transitive closure of LG-NTSCD as for slicing, could produce too few results to be useful.
7 EFSM Slicing with UNTICD
Backward static program slicing was first introduced by Weiser [Wei81] and describes a source code analysis technique that, through dependence relations, identifies all the statements in the program that influence the computation of a chosen variable and point in the program, i.e. the slicing criterion. It is non-termination insensitive. Similarly, EFSM slicing identifies those transitions which affect the slicing criterion, by computing control dependence and data dependence. Data dependence is a definition-clear path between a variable’s definition and use. We adopt the data dependence definition of [KSTV03] for an EFSM.
Definition 13 (Data Dependence (DD)). Ti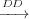 vTk means that transitions
Ti and Tk are data dependent with respect to variable v if:
vTk means that transitions
Ti and Tk are data dependent with respect to variable v if:
- v ∈ D(Ti), where D(Ti) is a set of variables defined by transition Ti, i.e. variables defined by actions and variables defined by the event of Ti that are not redefined in any action of Ti;
- v ∈ U(Tk), where U(Ti) is a set of variables used in a condition and actions of transition Ti;
- there exists a path in an EFSM from the source(Ti) to the target(Tk) whereby v is not modified.
The data dependences for the door controller EFSM in Figure 3 are: {T1 → T2,T3}, {T2 → T2,T3}, {T5 → T11}, {T8 → T11}, and {T11 → T11}.
Definition 14 (Slicing Criterion). A slicing criterion for an EFSM is a pair (t,V ) where transition t ∈ T and variable set V ⊆ V ar. It designates the point in the evaluation immediately after the execution of the action contained in transition t.
Definition 15 (Slice). A slice of an EFSM M, is an EFSM, M′, that contains ε-transitions. The transitions that are not ε-transitions are in the set of transitions that are directly or indirectly (transitive closure) DD and UNTICD on the slicing criterion c.
7.1 Computing EFSM slices
The objective of the slicing algorithm is to automatically compute the slice of an EFSM model M with respect to the given slicing criterion c. First, the algorithm computes the data dependences, using Definition 13, and the control dependences, using Definition 11, for all transitions in M. These are then represented in a dependence graph, which is a directed graph where nodes represent transitions and edges represent data and control dependences between transitions. Then, given the slicing criterion c, the algorithm marks all backwardly reachable transitions from c, i.e. the transitive closure of DD and UNTICD with respect to c. All unmarked transitions are anonymised i.e. become ε-transitions. Note that we can replace UNTICD, with NTICD, LG-NTSCD and NTSCD in order to compare the different slices produced.

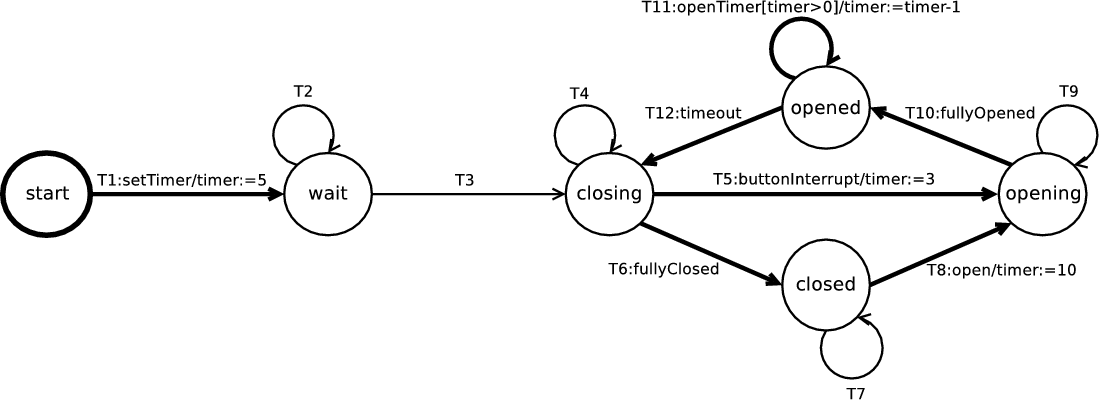
If the slicing criterion for the EFSM in Figure 3 is T11, then Figure 5(a) illustrates the slice produced when using UNTICD, and Figure 5(b) illustrates the slice produced when using LG-NTSCD. Unlike LG-NTSCD and NTSCD, UNTICD slicing slices away transitions which are affected by loops (before control sinks) that do not data dependent on T11, i.e. T3. Moreover, there are no LG-NTSCD dependences within the control sink because the transitions have trivial guards. Trivial guards in Figure 3 do not affect whether T10 and T9 will be taken non-deterministically, so in the case where event opening occurs infinitely, T11 is never reached. If the slicing criterion for the EFSM in Figure 3 is T12, then the marked transitions in the UNTICD slice are {T5,T10,T12}, while in the LG-NTSCD slice are {T3,T12}, in the NTSCD slice are {T3,T5,T10,T12} and in the NTICD slice is {T12}.
8 Conclusions
In this paper, we introduced a non-termination insensitive form of control dependence for EFSM slicing, that built on the recent work of Ranganath et al. [RAB+05] and subsumed Korel et al’s definition [KSTV03]. We demonstrated that by removing the fairness condition of Ranganath et al.’s NTICD no control dependences were removed, but extra control dependences within control sinks were introduced. Unlike NTICD our new definition works with non-terminating systems and, in general, produces smaller slices than those based on NTSCD.
References
[BH04] David Binkley and Mark Harman. A survey of empirical results on program slicing. Advances in Computers, 62:105–178, 2004.
[CCD98] Gerardo Canfora, Aniello Cimitile, and Andrea De Lucia. Conditioned program slicing. Information and Software Technology, 40(11):595–607, 1998.
[De 01] Andrea De Lucia. Program slicing: Methods and applications. In International Workshop on Source Code Analysis and Manipulation, pages 142–149, Los Alamitos, California, USA, 2001. IEEE Computer Society Press.
[GGRT06] Christophe Gaston, Pascale Le Gall, Nicolas Rapin, and Assia Touil. Symbolic execution techniques for test purpose definition. In Proceedings of Testing of Communicating Systems, pages 1–18. Springer, 2006.
[Har87] David Harel. Statecharts: A visual formalism for complex systems. Science of Computer Programming, 8(3):231–274, June 1987.
[HBD03] Mark Harman, David Binkley, and Sebastian Danicic. Amorphous program slicing. Journal of Systems and Software, 68(1):45–64, October 2003.
[HRB90] Susan Horwitz, Thomas Reps, and David Binkley. Interprocedural slicing using dependence graphs. ACM Transactions on Programming Languages and Systems, 12(1):26–61, 1990.
[HTW98] Mats P. E. Heimdahl, Jeffrey M. Thompson, and Michael W. Whalen. On the effectiveness of slicing hierarchical state machines: A case study. In EUROMICRO ’98: Proceedings of the 24th Conference on EUROMICRO, page 10435, Washington, DC, USA, 1998. IEEE Computer Society.
[HW97] Mats P. E. Heimdahl and Michael W. Whalen. Reduction and slicing of hierarchical state machines. In Proc. Fifth ACM SIGSOFT Symposium on the Foundations of Software Engineering. Springer–Verlag, 1997.
[Kam93] Mariam Kamkar. Interprocedural dynamic slicing with applications to debugging and testing. PhD Thesis, Department of Computer Science and Information Science, Link?ping University, Sweden, 1993.
[KSTV03] Bogdan Korel, Inderdeep Singh, Luay Tahat, and Boris Vaysburg. Slicing of state-based models. In Proceedings of the International Conference on Software Maintenance, pages 34–43, 2003.
[LG08] Sébastien Labbé and Jean-Pierre Gallois. Slicing communicating automata specifications: polynomial algorithms for model reduction. Formal Aspects of Computing, 2008.
[LGP07] Sebastien Labbe, Jean-Pierre Gallois, and Marc Pouzet. Slicing communicating automata specifications for efficient model reduction. In Proceedings of ASWEC, pages 191–200, USA, 2007. IEEE Computer Society.
[LH07] Sara Van Langenhove and Albert Hoogewijs. SVtL: System verification through logic tool support for verifying sliced hierarchical statecharts. In Lecture Notes in Computer Science, Recent Trends in Algebraic Development Techniques, pages 142–155. Springer Berlin / Heidelberg, 2007.
[LHHR94] N.G. Leveson, M.P.E. Heimdahl, H. Hildreth, and J.D. Reese. Requirements Specification for Process-Control Systems. IEEE Transactions on Software Engineering, 20(9):684–706, September 1994.
[RAB+05] Venkatesh Prasad Ranganath, Torben Amtoft, Anindya Banerjee, Matthew B. Dwyer, and John Hatcliff. A new foundation for control-dependence and slicing for modern program structures. In ESOP, pages 77–93, 2005.
[RAB+07] Venkatesh Prasad Ranganath, Torben Amtoft, Anindya Banerjee, John Hatcliff, and Matthew B. Dwyer. A new foundation for control dependence and slicing for modern program structures. ACM Trans. Program. Lang. Syst., 29(5):27, 2007.
[SW99] Frank Strobl and Alexander Wisspeintner. Specification of an elevator control system – an autofocus case study. Technical Report TUM-I9906, Technische Univerität München, 1999.
[Tip95] Frank Tip. A survey of program slicing techniques. Journal of Programming Languages, 3(3):121–189, September 1995.
[WDQ02] Ji Wang, Wei Dong, and Zhi-Chang Qi. Slicing hierarchical automata for model checking UML statecharts. In Proceedings of the 4th ICFEM, pages 435–446, UK, 2002. Springer-Verlag.
[Wei81] Mark Weiser. Program slicing. In 5th International Conference on Software Engineering, pages 439–449, San Diego, CA, March 1981.