Also available as: PDF.
Translations: Serbo-Croat.
Experimental Assessment of Software Metrics Using Automated Refactoring
ABSTRACT
A large number of software metrics have been proposed in the literature, but there is little understanding of how these metrics relate to one another. We propose a novel experimental technique, based on search-based refactoring, to assess software metrics and to explore relationships between them. Our goal is not to improve the program being refactored, but to assess the software metrics that guide the automated refactoring through repeated refactoring experiments.
We apply our approach to five popular cohesion metrics using eight real-world Java systems, involving 300,000 lines of code and over 3,000 refactorings. Our results demonstrate that cohesion metrics disagree with each other in 55% of cases, and show how our approach can be used to reveal novel and surprising insights into the software metrics under investigation.
1 Introduction
Metrics are used both implicitly and explicitly to measure and assess software [43], but it remains difficult to know how to assess the metrics themselves. Previous work in the metrics literature have suggested formal axiomatic analysis [45], though this approach is not without problems and limitations [18] and can only assess theoretical metric properties and not their practical aspects.
In this paper we introduce a novel experimental approach to the assessment of metrics, based on automated search-based refactoring. It is striking that many metrics purport to measure the same aspect of software quality, yet we have no way of checking these claims. For example, many metrics have been introduced in the literature that aim to measure software cohesion [9 11 26 33 20]. If these metrics were measuring the same property, then they ought to produce similar results. This poses some important but uncomfortable questions: how do the results of metrics that purport to measure the same software quality compare to one another? Can metrics that measure the same property disagree, and how strongly can they disagree? These questions are important, because we cannot rely on a suite of metrics to assess properties of software if we can neither determine the extent to which they agree, nor have any way to determine a likely worst case disagreement. They are also uncomfortable questions because, despite several decades of software metrics research and practice, there remains no answer, nor even an accepted approach to tackling them.
In this paper we address this problem by introducing an experimental technique to answer questions like these. Our approach applies automated refactoring to a program, repeatedly measuring the values of a number of metrics before and after applying each refactoring. In this way it is possible to make empirical observations about the relationships between the metrics. When a pair of metrics do not agree on the change brought about by a refactoring, we examine the causes of the conflict so as to gain a further (and more qualitative) insight into the differences between the metrics.
We evaluate our approach on five widely-used metrics for cohesion. We use a search-based, metric-guided refactoring platform, Code-Imp, that can apply a large number of refactorings without user intervention. Using Code-Imp, over 3,000 refactorings were applied to eight non-trivial, real-world Java programs comprising in total over 300,000 lines of code. For each refactoring, we compute before and after values for the cohesion metrics and analyse the results to obtain a quantitative and qualitative comparison of the metrics under assessment.
The primary contributions of this paper are as follows:
- The introduction of a new approach to metric analysis at the source code level. This implements the approach to metric investigation using search-based refactoring first proposed by Harman and Clark [25], but which has hitherto remained unimplemented.
- A case study showing how our approach reveals that seemingly similar metrics can be in conflict with one another, and can pinpoint the source of the conflict thus providing new insight into the differences between the metrics.
- The identification of a number of undocumented anomalies in established cohesion metrics, thereby demonstrating the utility of our approach as a means of investigating metrics.
This paper is structured as follows. In Section 2 we describe our experimental approach in more detail and in section 3 we outline the platform we use in this paper to perform search based refactoring. In section 4 we describe our initial investigation into how a suite of software metrics changes in response to refactoring, which leads to Section 5 where a detailed empirical comparison between two particular cohesion metrics is presented. Section 6 describes related work and finally, Section 7 concludes and describes future work. .
2 Motivation and Approach
The motivation for this work stems from a desire to “animate” metrics and observe their behaviour in relation to each other in a practical setting. A single software application allows only one set of metric measurements to be made. This is clearly not enough to make meaningful comparisons. A software repository such as CVS provides multiple versions of a software application and so serves as a better basis for comparison, and many studies have taken this approach [14 2 44]. However, a sequence of versions of a software application may vary wildly in terms of how great the gap is between each version. This lack of control over the differences between the versions is a significant confounding factor in studies that use software repositories to compare software metrics.
Our approach to this problem begins with the observation that individual refactorings in the style of Fowler [22] involve small behaviour-preserving program changes that typically have an impact on the values of software metrics that would be calculated for the program. For example, in applying the PushDownMethod refactoring, a method is moved from a superclass to those subclasses that require it. The superclass may become more cohesive if the method moved was weakly connected with the rest of the class. It may instead become less cohesive, if the moved method served to glue other methods and fields of the class together. It is impossible to state that the PushDownMethod refactoring leads to an increase or a decrease in cohesion without examining the context to which it is being applied. Furthermore, the impact the refactoring will have on the metric will depend on the precise notion of cohesion that the metric embodies.
The approach taken in this paper is to measure a set of metric values on a program, and then apply a sequence of refactorings to the program, measuring the metrics again after each refactoring is applied. Each refactoring represents a small, controlled change to the software, so it is possible to identify patterns in how the metric values change, and how they change in relation to each other. For N refactorings and M metrics, this approach provides a matrix of (N + 1) × M metric values. As will be demonstrated in sections 4 and 5, this matrix can be used to make a comparative, empirical assessment of the metrics and to detect areas of metric disagreement that can be subjected to closer examination.
An important issue in this approach is the manner in which the refactoring sequence itself is generated. The simplest solution is to apply a random sequence of refactorings to the program. However, most randomly-chosen refactorings can be expected to cause all software metrics to deteriorate, which is not of interest. In order to address this, we use the software metrics that are being studied to guide the refactoring process itself. In this way, we can ensure that a refactoring is applied only if it improves at least one of the metrics being studied. Crucially, each accepted refactoring will improve the cohesion of the program in terms of at least one of the metrics, though it may, in the extreme case, worsen it for all the other metrics.
This search-based approach to refactoring has already been used in many other studies [37 38 42 27 28 41 40 29 35 32]. In this paper, we use search-based refactoring not to achieve a goal in terms of refactoring the program, but to learn more about the metrics that are used to guide the refactoring process. The search-based refactoring tool we use, Code-Imp, is described in more detail in section 3.
The search-based algorithm we use to perform the refactoring is defined in figure 1. It is stochastic, as the pick operation makes a random choice of the class to be refactored, the refactoring type to be used and the actual refactoring to be applied. It is only necessary to run this search once on each software application, as each refactoring applied is a complete experiment in itself. The purpose of this algorithm is to give each class an equal chance of being refactored and to give each refactoring type (PullUpMethod, CollapseHierarchy, etc.) an equal chance of being applied. This is important in order to reduce the risk that bias in the refactoring process affects the observed behaviour of the metrics. The details of the fitness function are not defined in this algorithm, as they depend on the exact nature of what is being investigated. The fitness functions will be defined in sections 4 and 5 where the experiments are described in more detail.
Input: set of 14 refactoring types (e.g. PullUpMethod)
Input: set of metrics to be analysed
Output: metrics profile
refactoring_count = 0
repeat
while !empty(classes) do
refactoring_types = set of refactoring types
while !empty(refactoring_types) do
refactorings.populate(refactoring_type, class)
if !empty(refactorings) then
refactoring.apply()
if fitness_function_improves() then
update metrics profile
The functions used in this algorithm are defined as follows:
Set<element>::pick: removes and returns a it random
element from a set
Set<Refactoring>::populate(type, class): adds to the set all
legal refactorings of the given type on the given class
fitness_function_improves: Tests if the applied refactoring
has improved the software metrics. Details vary between
investigation 1 and investigation 2.
3 The Code-Imp Platform
Code-Imp is an extensible platform for metrics-driven search-based refactoring that has been previously used for automated design improvement [37 38]. It provides design-level refactorings such as moving methods around the class hierarchy, splitting classes and changing inheritance and delegation relationships. It does not support low-level refactorings that split or merge methods.
Code-Imp was developed on the RECODER platform [24] and
fully supports Java 6. It currently implements the following
refactorings [22]:
Method-level Refactorings
- Push Down Method:
- Moves a method from a class to those subclasses that require it.
- Pull Up Method:
- Moves a method from a class(es) to its immediate superclass.
- Increase/Decrease Method Accessibility:
- Changes the accessibility of a method by one level, e.g. public to protected or private to package.
Field-level Refactorings
- Push Down Field:
- Moves a field from a class to those subclasses that require it.
- Pull Up Field:
- Moves a field from a class(es) to their immediate superclass.
- Increase/Decrease Field Accessibility:
- Changes the accessibility of a field by one level, e.g. public to protected or private to package.
Class-level Refactorings
- Extract Hierarchy:
- Adds a new subclass to a non-leaf class C in an inheritance hierarchy. A subset of the subclasses of C will inherit from the new class.
- Collapse Hierarchy:
- Removes a non-leaf class from an inheritance hierarchy.
- Make Superclass Abstract:
- Declares a constructorless class explicitly abstract.
- Make Superclass Concrete:
- Removes the explicit ‘abstract’ declaration of an abstract class without abstract methods.
- Replace Inheritance with Delegation:
- Replaces an inheritance relationship between two classes with a delegation relationship; the former subclass will have a field of the type of the former superclass.
- Replace Delegation with Inheritance:
- Replaces a delegation relationship between two classes with an inheritance relationship; the delegating class becomes a subclass of the former delegate class.
Code-Imp parses the program to be refactored to produce a set of Abstract Syntax Trees (ASTs). It then repeatedly applies refactorings to the ASTs and regenerates the source code from the ASTs when the refactoring process is completed. Code-Imp decides on the next refactoring to perform based on the exact search technique in use and the value of the fitness function in use. The refactoring process can be driven using one of a number of metaheuristic search techniques, namely simulated annealing, hill climbing and a genetic algorithm. In this paper, only hill climbing is used.
The fitness function that guides the search is a computation based on one or more software metrics. Code-Imp provides two implementations for each metric related to the inclusion or exclusion of inheritance in the definition of the metric. Five cohesion metrics are used in this paper, namely Tight Class Cohesion (TCC) [8], Lack of Cohesion between Methods (LCOM5) [12], Class Cohesion (CC) [10], Sensitive Class Cohesion (SCOM) [21] and Low-level Similarity Base Class Cohesion (LSCC) [3]. The formal and informal definitions of these metrics are presented in Figure 2.
As with all automated approaches, the refactoring sequence generated by Code-Imp may not resemble the refactorings that a programmer would be inclined to undertake in practice. This issue is not relevant here as our focus is on the changes in the metric values, rather than the design changes brought about by the refactorings.
| |
||
| LSCC(c) | = 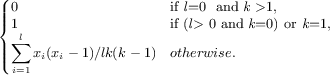 | The similarity between two methods is the collection of their direct and indirect shared attributes. |
| |
||
| TCC(c) | = 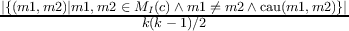 | Two Methods interact with each other if they directly or indirectly use an attribute of class c in common. |
| |
||
| CC(c) | = 2∑
i=1k-1 ∑
j=i+1k 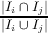 /k(k - 1) /k(k - 1) | The similarity between two methods is the ratio of the collection of their shared attributes to the total number of their referenced attributes. |
| |
||
| SCOM(c) | = 2∑
i=1k-1 ∑
j=i+1k 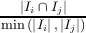 * *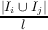 /k(k - 1) /k(k - 1) | The similarity between two methods is the ratio of the collection of their shared attributes to the minimum number of their referenced attributes. Connection intensity of a pair of methods is given more weight when such a pair involves more attributes. |
| |
||
| LCOM5(c) |
= 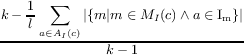 | Measures the lack of cohesion of a class in terms of the proportion of attributes each method references. Unlike the other metrics, LCOM5 measures lack of cohesion, so a lower value indicates better cohesion. |
| |
||
| |
|
|
| In the above: c is a particular class; MI(c) is the set of methods implemented in c; AI(c) is the set of attributes implemented in c; k and l are the number of methods and attributes implemented in class c respectively; Ii is the set of attributes referenced by method i; xi is the number of 1s in the ith column of the Method-Attribute Reference (MAR) matrix, MAR(i,j) holds 1 if ith method directly or indirectly references jth attribute; cau(m1,m2) holds 1 if m1 and m2 use an attribute of class c in common. |
|
|
|
|
.
4 Investigation I: general assessment of cohesion metrics
In this investigation we take a refactoring walk through the landscape of the range of cohesion metrics under consideration. Our goal is to gain an overall understanding of how the metrics change, and to seek out possible anomalous behaviour that can be investigated further.
As explained in section 2, random application of refactorings will usually cause deterioration in all cohesion metrics. We therefore use a search that cycles through the classes of the program under investigation as described in figure 1, and tries to find a refactoring on the class that improves at least one of the metrics being studied. The search will apply the first refactoring it finds that improves any metric. The other metrics may improve, stay the same, or deteriorate. Because this fitness function is easy to improve, we obtain the long refactoring sequences that are required to draw conclusions about relationships between metrics.
The metrics formulae presented in Figure 2 show how to calculate the metric for a single class. To measure the cohesion of a number of classes, i.e., an entire program, we use the formula for weighted cohesion based on that proposed by Briand and Al Dallal [2]:
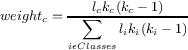
where weightn is the weight assigned to the cohesion of class n, ln is the number of attributes in class n, and kn is the number of methods in class n. In the case where kc equals 1, the numerator in the formula becomes l. This is the formula we use for LSCC. For other metrics we tailor this formula so it makes sense for that metric.
Most software metrics are ordinal in nature, so any formula that averages them is theoretically suspect. However, our experience suggests that these metrics are not far from being on an interval scale and so the risk in treating them as interval is slight in relation to the advantages that accrue. Briand et al. make a similar argument for the use of parametric methods for ordinal scale data [11].
| System | Description | LOC | #Classes
|
| JHotDraw 5.3 | Graphics | 14,577 | 208 |
| XOM 1.1 | XML API | 28,723 | 212 |
| ArtofIllusion 2.8.1 | 3D modeling | 87,352 | 459 |
| GanttProject 2.0.9 | Scheduling | 43,913 | 547 |
| JabRef 2.4.2 | Graphical | 61,966 | 675 |
| JRDF 0.4.1.1 | RDF API | 12,773 | 206 |
| JTar 1.2 | Compression | 9,010 | 59 |
| JGraphX 1.5.0.2 | Java Graphing | 48,810 | 229 |
| JHotDraw | JTar | XOM | JRDF | JabRef | JGraph | ArtOfIllusion | Gantt | All | |
| (1007) | (115) | (193) | (13) | (257) | (525) | (593) | (750) | (3453) | |
| LSCC | 96 | 99 | 100 | 92 | 99 | 100 | 99 | 96 | 98 |
| TCC | 86 | 53 | 97 | 46 | 61 | 72 | 84 | 71 | 78 |
| SCOM | 79 | 70 | 93 | 92 | 79 | 89 | 77 | 80 | 81 |
| CC | 100 | 98 | 100 | 92 | 99 | 100 | 100 | 99 | 100 |
| LCOM5 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 99 | 100 |
4.1 Results and Analysis
We applied this refactoring process to the eight open source Java projects presented in Table 1. In each case, the experiment was allowed to run for five days, or until a sequence of over 1000 refactorings was reached. In total, 3,453 refactorings were applied, as shown in Table 2. The applications were of high quality initially, so improvements to cohesion were time-consuming to find. JHotDraw proved the easiest program to refactor because its extensive use of design patterns and a rich inheritance hierarchy provided plenty of opportunity to refactor. Note that in this work we are using the refactoring process only to investigate the properties of the metrics. We make no claim that the refactored program has a better design than the original program. .
4.1.1 Volatility
One aspect of a metric that this investigation allows us to see is its volatility. A volatile metric is one that is changed often by refactorings, whereas an inert metric is one that is changed infrequently by refactorings. Volatility is an important factor in determining the usefulness of a metric. For example, in search-based refactoring, a highly volatile metric will have a very strong impact on how the refactoring proceeds while a relatively inert metric may simply be pointless to compute. In a software quality context, measuring the improvement in a system’s design using a set of inert metrics is likely to be futile, as they are, by definition, crude measures that do not detect subtle changes in the property they measure. Table 2 shows the volatility of the 5 metrics in each individual system under investigation, and averaged across all systems.
The first observation is that LSCC, CC and LCOM5 are all highly volatile metrics. In 99% of the refactorings applied across all applications, each these metrics either increased or decreased. The relative lack of volatility of the TCC metric is largely due to the cau relation (see Figure 2), which holds relatively rarely for any given pair of methods.
The results for the JRDF application are notable. All metrics bar TCC are highly volatile for this application. Although JRDF is one of the larger applications, a total of only 13 refactorings could be applied to it, compared to the 1000+ refactorings that could be applied to JHotDraw, a similarly-sized application. The explanation for this lies in the nature of the applications. In JHotDraw, 86% of the classes are subclasses, whereas in JRDF this figure is only 6%. Since most of the refactorings Code-Imp applies relate to inheritance, an application that makes little use of inheritance provides few opportunities to refactor.
While there is some consistency across the different applications, the JRDF example illustrates that, given an individual metric, volatility can vary substantially between systems. We attempted normalising the volatilities against the overall volatility of each application, and, while this improved the consistency somewhat, a large variance remained. We thus conclude that volatility is dependent on a combination of a metric and the application to which it is applied.
| JHotDraw | JTar | XOM | JRDF | JabRef | JGraph | ArtOfIllusion | GanttProject | Average | |
| LSCC | ↑50 , 46↓ | ↑50 , 49↓ | ↑57 , 43↓ | ↑46 , 46↓ | ↑54 , 46↓ | ↑51 , 48↓ | ↑57 , 42↓ | ↑53 , 43↓ | ↑53 , 45↓ |
| TCC | ↑45 , 41↓ | ↑30 , 23↓ | ↑51 , 46↓ | ↑23 , 23↓ | ↑34 , 27↓ | ↑37 , 35↓ | ↑52 , 35↓ | ↑39 , 31↓ | ↑43 , 35↓ |
| SCOM | ↑38 , 40↓ | ↑34 , 36↓ | ↑50 , 44↓ | ↑46 , 46↓ | ↑37 , 42↓ | ↑36 , 53↓ | ↑44 , 33↓ | ↑40 , 40↓ | ↑40 , 41↓ |
| CC | ↑53 , 47↓ | ↑52 , 46↓ | ↑51 , 49↓ | ↑46 , 46↓ | ↑54 , 44↓ | ↑61 , 39↓ | ↑58 , 42↓ | ↑57 , 42↓ | ↑56 , 44↓ |
| LCOM5 | ↑51 , 49↓ | ↑50 , 50↓ | ↑48 , 52↓ | ↑54 , 46↓ | ↑49 , 50↓ | ↑41 , 59↓ | ↑56 , 43↓ | ↑50 , 50↓ | ↑50 , 50↓ |
4.1.2 Probability of positive change
Table 2 shows how volatile the metrics are, but it does not show whether the volatility is in a positive or negative sense. In Table 3 we present this view of the metrics. Recall that every refactoring applied in this investigation increases at least one of the cohesion metrics. It is remarkable then to note how often an increase in one cohesion metric leads to a decrease in another. Taking LSCC and ArtOfIllusion as an example, LSCC decreases in 42% of the refactorings (593 in total). So for ArtOfIllusion, 249 refactorings that improved at least one of TCC, SCOM, CC or LCOM5, as guaranteed by the refactoring process, caused LSCC to worsen.
| LSCC | TCC | SCOM | CC | |
| TCC | 0.60 | |||
| SCOM | 0.70 | 0.58 | ||
| CC | 0.10 | 0.01 | -0.28 | |
| LCOM5 | -0.17 | -0.21 | -0.46 | 0.72 |
This pattern of conflict is repeated across Table 3. As summarised in Table 4, TCC, LSCC and SCOM exhibit collective moderate positive correlation, while CC and LCOM5 show mixed correlation ranging from moderate positive correlation (LCOM5 and SCOM) to strong negative correlation (LCOM5 and CC).
In order to summarise the level of disagreement across the set
of metrics, we also considered each pairwise comparison
between each pair of metrics for each refactoring. For 5
metrics we have (5 * 4)∕2 = 10 pairwise comparisons per
refactoring. For 3,453 refactorings, this yields a total of
34,530 pairwise comparisons. Each pair is categorised as
follows:
Dissonant: One value increases or decreases, while the other stays the same.
Conflicted: One value increases, while the other decreases.
Across the entire set of refactorings, we found the levels to be as follows: 45% agreement, 17% dissonant and 38% conflicted. The figure of 38% conflicted is remarkable and indicates that, in a significant number of cases, what one cohesion metric regards as an improvement in cohesion, another cohesion metric regards as a decrease in cohesion. This has a practical impact on how cohesion metrics are used. Trying to improve a software system using a combination of conflicted cohesion metrics is impossible — an improvement in terms of one cohesion metric is likely to cause a deterioration in terms of another metric. .
4.2 Summary
This investigation has served to show the variance between software cohesion metrics in terms of their volatility and their propensity to agree or disagree with each other. Of course a cohesion metric that completely agrees with another makes no contribution to the cohesion debate. However, the conflict between the metrics indicates that the suite of cohesion metrics do not simply reflect different aspects of cohesion, they reflect contradictory interpretations of cohesion.
In order to investigate this conflict further, we choose two cohesion metrics, LSCC and TCC, and analyse them in greater detail using search-based refactoring. The results of this are presented in the following section. .
5 Investigation II: detailed analysis of cohesion metrics
The first investigation shows how search-based refactoring can be used to create a broad-stroke picture of how metrics relate to each other. In this second investigation we take two well-known cohesion metrics, LSCC and TCC, and explore their relationship more closely. We choose these two metrics as they are popular, low-level design metrics that have different characteristics. TCC was published in 1995 by Bieman and Kang [8], has stood the test of time, and was found to be rather inert in investigation I. LSCC was published in 2010 by Briand and Al Dallal [2], and hence represents a very recent interpretation of cohesion. In constrast to TCC, LSCC was found to be very volatile in investigation I.
In the definition of both these metrics [8 2], the respective authors mention the issue of whether or not inheritance should be considered in calculating cohesion, but do not discuss it in detail. If inheritance is taken into account, then the cohesion of a class is calculated as if all inherited methods and fields were part of the class as well. In the view of the authors of this present paper, this is a critical issue. A class might appear to have two unrelated methods, but if they both access the same inherited methods or fields they might in fact be very cohesive1. Hence we consider two versions of each of these metrics, the normal, ‘local’ versions termed LSCC and TCC, and the ‘inherited’ versions, which we term LSCCi and TCCi.
We conducted two experiments to test the relationships between these metrics. In each experiment, we use one metric to drive the refactoring process, and measure the impact on another metric. The experiments are as follows:
- increase LSCC measure TCC
- increase TCCi measure LSCCi
The other obvious experiments, increasing TCC and measuring LSCC and increasing LSCCi measuring TCCi were also performed. The results were in keeping with what we report below, but the details are omitted for space reasons. JHotDraw was chosen as the application on which to run these experiments as it proved in Section 4 to be the application that Code-Imp found easiest to refactor.
We alter the fitness function used to drive the search in these experiments. In our initial investigations in Section 4 the goal was to apply as many refactorings as possible to gain an overall view of the metric interactions. By contrast, in this section we wish to mimic a developer refactoring a program using a cohesion metric as guidance. If we use average class cohesion as the fitness function, we ignore the fact that, from a software engineering perspective, classes are not all of the same importance. For example, it is more useful to improve the cohesion of a frequently-updated class than of a stable class.
For these reasons we use a novel fitness function in the domain of search-based refactoring: a Pareto-optimal search across the classes of the program being refactored2. A refactoring that attempts to increase a metric is only accepted if it increases that metric for at least one class, and causes no decline in that metric for any other class. This is quite a limiting fitness function, but we argue that the resulting refactoring sequence is likely to be acceptable as a useful refactoring sequence in practice. The lengths of the refactoring sequences in these experiments are much shorter than those in Section 4, but are of sufficient length for trends to be observed.
5.1 Increasing LSCC, measuring TCC
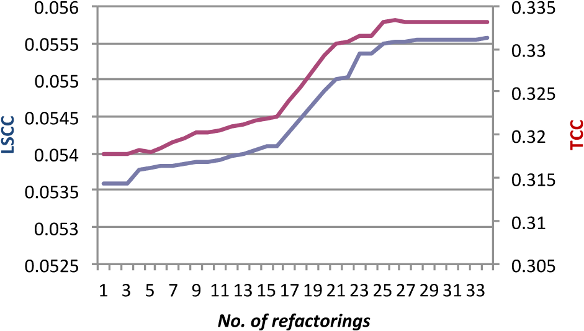
The result of refactoring JHotDraw to improve LSCC and measuring the impact on TCC is presented in Figures 3 and 4. 33 refactorings are performed and both metrics increase steadily and with little apparent conflict (Spearman rank correlation 0.8). However, when we look more closely at the refactorings in Figure 3, an anomaly becomes apparent. At refactoring 26, TCC drops slightly and remains constant for the next 5 refactorings, while LSCC steadily increases. We examine this area of disagreement more closely to determine what it tell us about the metrics.
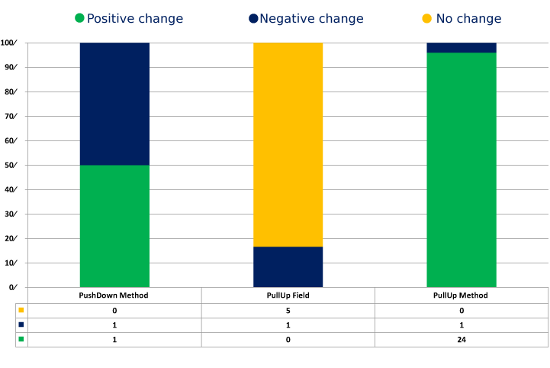
This period of disagreement occurs during a sequence of PullUpField refactorings where the target class has no fields. TCC is undefined for a class with no fields, so moving a field to such a class appears to reduce cohesion by adding a class with zero cohesion to the program. On the other hand, we learn from this example that LSCC prefers to move a field that is loosely associated with a class (e.g. used directly or indirectly by only one method) to its superclass, if that superclass has a zero LSCC measure (no two methods access the same field). In practice, this would be viewed as a detrimental refactoring, so we have uncovered a weakness in the LSCC metric that it would reward such a refactoring. .
5.2 Increasing TCCi, measuring LSCCi
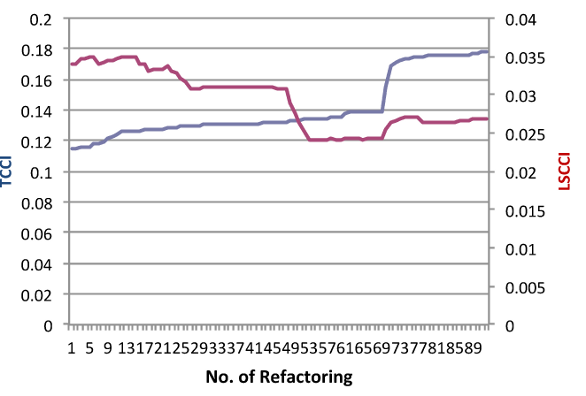
The result of refactoring JHotDraw to improve TCCi and measuring the impact on LSCCi is presented in Figure 5. 91 refactorings were performed and while there is some agreement in places, overall the graph shows extreme conflict (Spearman rank correlation -0.8).
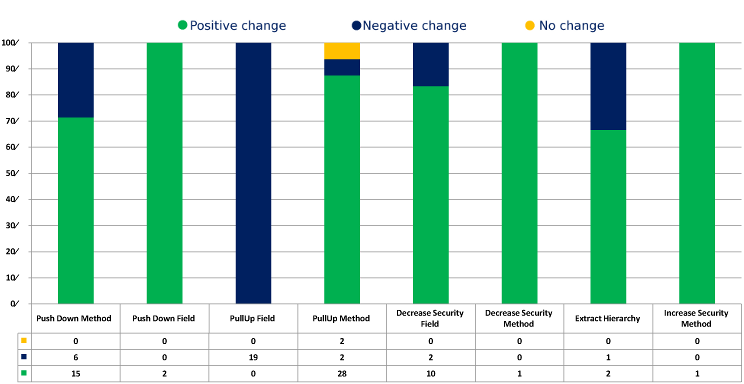
Figure 6 provides a detailed view of the refactorings and their effect on the LSCCi metric. The most striking feature is that PullUp Field has a negative impact on LSCCi in every case. The negative impact occurs because a field is moved to a superclass where it has no interaction which reduces LSCCi for that class. TCCi favours this refactoring because as part of pulling a private field up to a superclass, it must be made protected, and this causes more interaction between protected methods that use the field in the hierarchy structure. This use of PullUp Field in this case does truly improve cohesion, so it is a strength of LSCCi that it would not recommend it.
Another area of conflict is the negative effect PushDown Method has on LSCCi in six refactorings. On inspecting these refactorings, we learn that TCCi always prefers a method to reside in a class where it is used and access the fields it needs in its superclass (where they cannot be private of course), rather than reside in the superclass. However, LSCCi places more emphasis on keeping fields private, so it frequently prefers a method to stay in the class of the fields it uses except where the method is used by majority of the subclasses.
5.3 Summary
In this section we used a Pareto-optimal search across classes in order to demonstrate how two metrics can be compared and contrasted in a detailed way. In both experiments, LSCC vs. TCC and TCCi vs. LSCCi, we found areas of agreement and conflict between the metrics. Examining the areas of conflict more closely shed light on aspects of the metrics that are not readily apparent from their formulae.
6 Related Work
In this section we review related work in Search-Based Refactoring (section 6.1) and Software Metrics (section 6.2).
6.1 Search-Based Refactoring
Search-based refactoring is fully automated refactoring driven by metaheuristic search and guided by software quality metrics, as introduced by O’Keeffe and Ó Cinnéide [39]. Existing work in this area uses either a ‘direct’ or an ‘indirect’ approach. In the direct approach the refactoring steps are applied directly to the program, denoting moves from the current program to a near neighbour in the search space. Early examples of the direct approach are the works by Williams [46] and Nisbet [34] who addressed the parallelization problem. More recently, O’Keeffe and Ó Cinnéide [37 38] applied the direct approach to the problem of automating design improvement.
In the indirect approach, the program is indirectly optimised through the optimisation of the sequence of transformations to apply to the program. In this approach fitness is computed by applying the sequence of transformations to the program in question and measuring the improvement in the metrics of interest. The first authors to use search in this way were Cooper et al. [13], who used biased random sampling to search a space of high-level whole-program transformations for compiler optimisation. Also following the indirect approach, Fatiregun et al. [16 17] showed how search based transformations could be used to reduce code size and construct amorphous program slices.
Seng et al. [42] propose an indirect search-based technique that uses a genetic algorithm over refactoring sequences. In contrast to O’Keeffe and Ó Cinnéide [36], their fitness function is based on well-known measures of coupling between program components. Both these approaches used weighted-sum to combine metrics into a fitness function, which is of practical value but is a questionable operation on ordinal metric values. A solution to the problem of combining ordinal metrics was presented by Harman and Tratt, who introduced the concept of Pareto optimality to search-based refactoring [27]. They used it to combine two metrics into a fitness function and demonstrated that it has several advantages over the weighted-sum approach.
The work of Sahraoui et al. [41] has some similarities to ours, notably their premise that semi-automated refactoring can improve metrics. Their approach is to seek to gain insight into the refactorings that are chosen to improve a chosen metric. Our approach is the reverse of this: we use refactorings to gain insights into (multiple) metrics.
In recent work, Otero et al. [40] use search-based refactoring to refactor a program as it is being evolved using genetic programming in an attempt to find a different design which may admit a useful transformation as part of the genetic programming algorithm. Jensen and Cheng [29] use genetic programming to drive a search-based refactoring process that aims to introduce design patterns. Ó Cinnéide et al. use a search-based refactoring approach to try to improve program testability [35]. Kilic et al. explore the use of a variety of population-based approaches to search-based parallel refactoring, finding that local beam search could find the best solutions [32]. .
6.2 Analysis of Software Metrics
One criticism that is levelled at the use of software metrics is that they often fail to measure what they purport to measure [20]. This has led to a proliferation of software metrics [19], many of which attempt to measure the same aspect(s) of code. It is not surprising then that several studies have attempted to compare software metrics to better understand their similarities and differences. In this section, we focus on studies that have analysed cohesion metrics. The overriding problem with cohesion (and its measurement) has been that, unlike coupling, any metric claiming to measure cohesion is relatively subjective and open to interpretation [15]. Most cohesion measures have focused on the distribution of attributes in the methods of a class (and variations thereof). However, nuances of different object-oriented languages and the fact that the distribution of attributes can make it impossible to calculate cohesion metrics, means that no single, agreed cohesion metric exists.
The LCOM metric has been subject to detailed scrutiny [12] and revised several times to account for idiosyncrasies in its calculation. Comparisons between LCOM and other proposed cohesion metrics are a common feature of empirical studies [1 2 3 7 8 14]. Most newly-proposed cohesion-based metrics have attempted to improve upon previous metrics by forming a link between low cohesion and high fault-proneness [2 3] or intuitive notions of high cohesion and subjective developer views of what constitutes high cohesion [7]; others have tried to demonstrate a theoretical improvement [1 14]. Comparison of cohesion metrics has been a consistent topic for research [30 31 44]. For example, the Cohesion Amongst the Methods of a Class (CAMC) metric [7] provides a variation on the LCOM metric by including the self property in C++ in its calculation, and has been validated against developer opinion.
Al Dallal and Briand [1] investigated the relationship between their proposed metric, Low-Level Similarity-Based Class Cohesion (LSCC), and eleven other low-level cohesion metrics in terms of correlation and ability to predict faults. Based on correlation studies they concluded that LSCC captures a cohesion measurement dimension of its own. Four open source Java applications consisting of 2,035 classes and over 200KLOC were used as a basis of their study.
Counsell et al. [14] proposed a new metric called the Normalized Hamming Distance Metric (NHD). The authors concluded that NHD is a better cohesion metric than CAMC. Their empirical data, obtained from three C++ applications, showed a strong negative correlation between NHD and other metrics. This contrasts with a more recent study by Kaur and Singh [31] who explored the relationship between NHD, SNHD [14] and CAMC. They observed that class size was a confounding factor in the computation of both CAMC and NHD.
Alshayeb discovered that refactoring had a positive effect on several cohesion metrics in his study of open source software [6]. However, in later work he reported that this effect was not necessarily positive on other external software quality attributes such as reusability, understandability, maintainability, testability and adaptability [5]. An information-theoretic approach to measuring cohesion was proposed by Khoshgoftaar et al. [4] and while this represented a fresh approach to cohesion measurement, their metric is subject to the same criticisms as previous metrics.
These studies have created a deeper understanding of software metrics and have shown that metrics with a similar intent do not necessarily provide similar results. However, understanding the underlying characteristics of a metric is just a first step in determining their usefulness. The approach detailed in this paper takes the next step by quantifying the extent of conflict between metrics to pinpoint the root cause of that conflict. .
7 Conclusions and Future Work
In this paper we use search-based refactoring for a novel purpose: to discover relationships between software metrics. By using a variety of search techniques (semi-random search, Pareto-optimal search on classes) guided by a number of cohesion metrics, we are able to make empirical assessments of the metrics. In areas of direct conflict between metrics, we examine the refactorings that caused the conflict in order to learn more about nature of the conflict.
In our study of 300KLOC of open source software we found that the cohesion metrics LSCC, TCC, CC, SCOM and LCOM5 agreed with each other in only 45% of the refactorings applied. In 17% of cases dissonance was observed (one metric changing while the other remains static) and in 38% of cases the metrics were found to be in direct conflict (one metric improving while the other disimproves). This high percentage of conflict reveals an important feature of cohesion metrics: they not only embody different notions of cohesion, they embody conflicting notions of cohesion. This key result refutes the possibility of ever creating a single, unifying cohesion metric.
In three areas of conflict between LSCC and TCC our analysis of the refactorings led to detailed insights into the differences between these metrics (see sections 5.1 and 5.2). This analysis also demonstrated that the decision of whether or not to include inheritance in the definition of a cohesion metric is not simply a matter of taste as has been hitherto assumed [8 2] — LSCC and TCC largely agree while their inherited versions exhibit extreme conflict. Our goal in this work is not to resolve these issues, but to provide a methodology whereby they can be detected in order to aid further metrics research. In some cases, software design principles indicate which metric is best. In other cases, the developer can choose which metric best suits their needs.
We claim that this approach can contribute significantly to the ongoing metrics debate. It provides a platform upon which metrics can be animated and their areas of agreement and disagreement brought into clear focus. Future work in this area involves performing the analysis using a broader range of searches, e.g. using two metrics, try to refactor to increase their disagreement, or refactor to worsen a metric as much as possible, before refactoring to improve it again, as well as applying this approach to other metrics, most obviously coupling metrics. Another area for further research is the analysis of the refactorings that cause metrics to conflict. This analysis was performed by hand in this paper, but attempting to automate it is an interesting research challenge.
8 Acknowledgments
This research is partly funded by the Irish Government’s Programme for Research in Third-Level Institutions through the Lero Graduate School in Software Engineering.
9 References
[1] J. Al Dallal. Validating object-oriented class cohesion metrics mathematically. In SEPADS’10, USA, 2010.
[2] J. Al Dallal and L. Briand. A precise method-method interaction-based cohesion metric for object-oriented classes. ACM Transactions on Software Engineering and Methodology, 2010.
[3] J. Al-Dallal and L. C. Briand. An object-oriented high-level design-based class cohesion metric. Information & Software Technology, 52(12):1346–1361, 2010.
[4] E. B. Allen, T. M. Khoshgoftaar, and Y. Chen. Measuring coupling and cohesion of software modules: an information-theory approach. Proceedings Seventh International Software Metrics Symposium, (561):124–134, 2001.
[5] M. Alshayeb. Empirical investigation of refactoring effect on software quality. Information & Software Technology, 51(9):1319–1326, 2009.
[6] M. Alshayeb. Refactoring effect on cohesion metrics. In International Conference on Computing, Engineering and Information, 2009. ICC ’09, Apr. 2009.
[7] J. Bansiya, L. Etzkorn, C. Davis, and W. Li. A class cohesion metric for object-oriented designs. Journal of Object Oriented Programming, 11(08):47–52, 1999.
[8] J. M. Bieman and B.-K. Kang. Cohesion and reuse in an object-oriented system. In Symposium on Software reusability, Seattle, Washington, 1995.
[9] J. M. Bieman and L. M. Ott. Measuring functional cohesion. IEEE Transactions on Software Engineering, 20(8):644–657, Aug. 1994.
[10] C. Bonja and E. Kidanmariam. Metrics for class cohesion and similarity between methods. In Proceedings of the 44th annual Southeast regional conference, pages 91–95, Florida, 2006. ACM.
[11] L. Briand, K. E. Emam, and S. Morasca. On the application of measurement theory in software engineering. Empirical Software Engineering, 1:61–88, 1996.
[12] L. C. Briand, J. W. Daly, and J. Wüst. A unified framework for cohesion measurement in object-oriented systems. Empirical Software Engineering, 3(1):65–117, 1998.
[13] K. D. Cooper, P. J. Schielke, and D. Subramanian. Optimizing for reduced code space using genetic algorithms. In Proceedings of LCTES’99, volume 34.7 of ACM Sigplan Notices, pages 1–9, NY, May 5 1999.
[14] S. Counsell, S. Swift, and J. Crampton. The interpretation and utility of three cohesion metrics for object-oriented design. ACM Trans. Softw. Eng. Methodol., 15(2):123–149, 2006.
[15] S. Counsell, S. Swift, and A. Tucker. Object-oriented cohesion as a surrogate of software comprehension: an empirical study. In Proceedings of the Fifth IEEE International Workshop on Source Code Analysis and Manipulation, SCAM ’05, pages 161–172, Washington, DC, USA, 2005. IEEE Computer Society.
[16] D. Fatiregun, M. Harman, and R. Hierons. Evolving transformation sequences using genetic algorithms. In SCAM 04, pages 65–74, Los Alamitos, California, USA, Sept. 2004. IEEE Computer Society Press.
[17] D. Fatiregun, M. Harman, and R. Hierons. Search-based amorphous slicing. In WCRE 05, pages 3–12, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA, Nov. 2005.
[18] N. E. Fenton. Software measurement: A necessary scientific basis. IEEE Transactions on Software Engineering, 20(3):199–206, 1994.
[19] N. E. Fenton and M. Neil. Software metrics: Roadmap. pages 357–370. ACM Press, 2000.
[20] N. E. Fenton and S. L. Pfleeger. Software metrics - a practical and rigorous approach (2. ed.). International Thomson, 1996.
[21] L. Fernández and R. P. na. A sensitive metric of class cohesion. Information Theories and Applications, 13(1):82–91, 2006.
[22] M. Fowler, K. Beck, J. Brant, W. Opdyke, and D. Roberts. Refactoring: Improving the Design of Existing Code. Addison-Wesley, 1999.
[23] E. Gamma, R. Helm, R. E. Johnson, and J. Vlissides. Design Patterns: Elements of Reusable Object-Oriented Software. Addison-Wesley, Reading, MA, 1995.
[24] T. Gutzmann et al. Recoder: a java metaprogramming framework, March 2010. http://sourceforge.net/projects/recoder.
[25] M. Harman and J. Clark. Metrics are fitness functions too. In Proc. International Symposium on METRICS, pages 58–69, USA, 2004. IEEE Computer Society.
[26] M. Harman, S. Danicic, B. Sivagurunathan, B. Jones, and Y. Sivagurunathan. Cohesion metrics. In 8th International Quality Week, pages Paper 3–T–2, pp 1–14, San Francisco, May 1995.
[27] M. Harman and L. Tratt. Pareto optimal search based refactoring at the design level. In Proceedings GECCO 2007, pages 1106–1113, July 2007.
[28] I. Hemati Moghadam and M. Ó Cinnéide. Automated refactoring using design differencing. In Proc. of European Conference on Software Maintenance and Reengineering, Szeged, Mar. 2012.
[29] A. Jensen and B. Cheng. On the use of genetic programming for automated refactoring and the introduction of design patterns. In Proceedings of GECCO. ACM, July 2010.
[30] P. Joshi and R. K. Joshi. Quality analysis of object oriented cohesion metrics. In QUATIC’10, pages 319–324. IEEE Computer Society, Oct. 2010.
[31] K. Kaur and H. Singh. Exploring design level class cohesion metrics. Journal of Software Engineering and Applications, 03(04):384–390, 2010.
[32] H. Kilic, E. Koc, and I. Cereci. Search-based parallel refactoring using population-based direct approaches. In Proceedings of the Third international Conference on Search Based Software Engineering, SSBSE’11, pages 271–272, 2011.
[33] A. Lakhotia. Rule–based approach to computing module cohesion. In Proceedings of the 15th Conference on Software Engineering (ICSE-15), pages 34–44, 1993.
[34] A. Nisbet. GAPS: A compiler framework for genetic algorithm (GA) optimised parallelisation. In P. M. A. Sloot, M. Bubak, and L. O. Hertzberger, editors, High-Performance Computing and Networking, International Conference and Exhibition, HPCN Europe 1998, Amsterdam, The Netherlands, April 21-23, 1998, Proceedings, volume LNCS 1401, pages 987–989. Springer, 1998.
[35] M. Ó Cinnéide, D. Boyle, and I. Hemati Moghadam. Automated refactoring for testability. In Proceedings of the International Conference on Software Testing, Verification and Validation Workshops (ICSTW 2011), Berlin, Mar. 2011.
[36] M. O’Keeffe and M. Ó Cinnéide. Search-based software maintenance. In CSMR’06, Mar. 2006.
[37] M. O’Keeffe and M. Ó Cinnéide. Search-based refactoring: an empirical study. J. Softw. Maint. Evol., 20(5):345–364, 2008.
[38] M. O’Keeffe and M. Ó Cinnéide. Search-based refactoring for software maintenance. J. Syst. Softw., 81(4):502–516, 2008.
[39] M. O’Keeffe and M. Ó Cinnéide. A stochastic approach to automated design improvement. In PPPJ’03, pages 59–62, Kilkenny, June 2003.
[40] F. E. B. Otero, C. G. Johnson, A. A. Freitas, , and S. J. Thompson. Refactoring in automatically generated programs. Search Based Software Engineering, International Symposium on, 0, 2010.
[41] H. Sahraoui, R. Godin, and T. Miceli. Can metrics help to bridge the gap between the improvement of OO design quality and its automation? In ICSM’00, pages 154–162, Oct. 2000.
[42] O. Seng, J. Stammel, and D. Burkhart. Search-based determination of refactorings for improving the class structure of object-oriented systems. In GECCO ’06, Seattle, Washington, USA, 8-12 July 2006. ACM.
[43] M. J. Shepperd. Foundations of software measurement. Prentice Hall, 1995.
[44] G. Succi, W. Pedrycz, S. Djokic, P. Zuliani, and B. Russo. An empirical exploration of the distributions of the chidamber and kemerer object-oriented metrics suite. Empirical Software Engineering, 10(1):81–104, 2005.
[45] E. J. Weyuker. Evaluating software complexity measures. IEEE Transactions on Software Engineering, 14(9):1357–1365, Sept. 1988.
[46] K. P. Williams. Evolutionary Algorithms for Automatic Parallelization. PhD thesis, University of Reading, UK, Sept. 1998.